轉:策略價值:在思辨中自(zì)主感悟──“解決問(wèn)題的策略”教學片段與思考
“思辨”,即“思考辨析”,它首先指的是一種思考方式。思辨往往涉及分(fēn)析、辨别、推理(lǐ)、判斷、表述、交流等數學思維過程和活動,它不僅是學生(shēng)數學思維綜合能力強弱的一種體(tǐ)現,更是學生(shēng)數學素養水平高低的一種象征。因此,在教學中,教師(shī)要從(cóng)學生(shēng)的認知基礎和學習經驗出發,引導學生(shēng)對知識進行主動建構,對學習過程進行主動思辨,從(cóng)而實現數學知識的内化理(lǐ)解。
蘇教版小學數學教材從(cóng)三年級起,每冊安排一個單元,相(xiàng)對集中地教學“解決問(wèn)題的策略”。對于學生(shēng)而言,接受某一種策略的概念并不困難,困難的是如(rú)何經曆策略的形成過程。“解決問(wèn)題的策略”的教學,教師(shī)不能僅僅關注具體(tǐ)問(wèn)題的解法和結論,而應該引導學生(shēng)通過對一系列問(wèn)題的思辨,認識策略的特點和價值,形成主動運用策略的意識,從(cóng)而進一步發展思維的條理(lǐ)性和嚴密性,提高分(fēn)析問(wèn)題和解決問(wèn)題的能力。現結合蘇教版數學五年級上冊“解決問(wèn)題的策略──列舉”一課的教學片段,談談自(zì)己的實踐與思考。
【教學片段】
出示例題:王大(dà)叔用22根1米長的木條圍一個長方形花圃,怎樣圍面積最大(dà)?
師(shī) 根據題目的條件(jiàn)和問(wèn)題,你(nǐ)知道了什麽?
……
師(shī) 如(rú)果用22根同樣長的小棒表示這22根1米長的木條,你(nǐ)能試着擺出一個符合要求的長方形嗎(ma)?
生(shēng) 我圍成的長方形長是8米,寬是3米。
師(shī) 判斷一下,他(tā)圍成的這個長方形符不符合題目條件(jiàn)?
生(shēng) 長方形的周長是22米,說(shuō)明一條長和一條寬的和是22÷2=11(米),而8+3=11(米),正好符合條件(jiàn)。
師(shī) 剛才同學們找到了一種圍法,那還(hái)有沒有其他(tā)圍法?怎樣圍才能使長方形的面積最大(dà)呢(ne)?
生(shēng) 隻要把所有的圍法都(dōu)找出來(lái),計(jì)算出面積後再進行比較就(jiù)可(kě)以了。
師(shī) 對啊,要知道怎樣圍面積最大(dà),就(jiù)需把各種圍法一一列舉出來(lái)進行比較。同學們試着自(zì)己解決,然後小組交流。
師(shī) (出示圖1)這個同學找到了幾種不同的圍法?面積最大(dà)是多少?
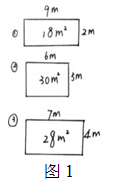
生(shēng) 找到了3種圍法,面積最大(dà)是30平方米。
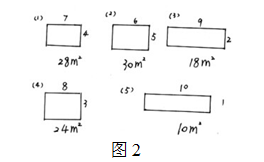
師(shī) 而這個同學找到了5種不同的圍法(圖2),與剛才相(xiàng)比多了哪兩種圍法?
生(shēng) 多了長是10米,寬是1米;長是8米,寬是3米的兩種圍法。
師(shī) 這兩種圍法都(dōu)符合題目條件(jiàn)嗎(ma)?他(tā)找到的長方形面積最大(dà)是多少?
生(shēng) 都(dōu)符合,因爲10米加上1米等于11米,8米加上3米也等于11米,都(dōu)是長方形周長的一半。這樣找到長方形的面積最大(dà)是30平方米。
師(shī) 繼續看(kàn),這位同學也找到了5種不同的圍法(圖3),長方形的面積最大(dà)也是30平方米。比較一下,他(tā)們在找的過程中什麽不同?
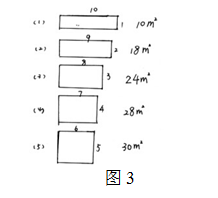
生(shēng) 前一種沒有按照(zhào)一定的順序來(lái)找,而後一種是按照(zhào)一定的順序來(lái)找的,長從(cóng)大(dà)到小,寬從(cóng)小到大(dà),比較有規律。
師(shī) 同學們觀察得(de)非常仔細,像這樣寬是1米、長是10米;寬是2米、長是9米……就(jiù)是一種有序的找法(闆書(shū):有序),而像前一種(圖2)就(jiù)是無序的找法。相(xiàng)比較而言,你(nǐ)更欣賞哪一種?
生(shēng) 我更欣賞後一種,因爲找的時候比較有序,這樣就(jiù)不會出現遺漏的情況。
師(shī) 對啊,有序地去(qù)找,答案就(jiù)不容易遺漏。(闆書(shū):不遺漏)
師(shī) (出示圖4)同樣是有序地找,可(kě)是這個同學爲什麽卻找到了10種圍法?
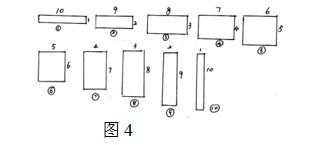
生(shēng) 從(cóng)第6種圍法開始就(jiù)重複了,如(rú)果把後面的長方形橫過來(lái),其實就(jiù)和前面的長方形一樣。
師(shī) 說(shuō)得(de)非常有道理(lǐ)。那麽在有序找的過程中,我們應該找到什麽時候爲止呢(ne)?
生(shēng) 當後一個長方形的長與前一個長方形的寬一樣的時候,往下找就(jiù)重複了。
師(shī) 看(kàn)來(lái),我們在有序找的時候,還(hái)要注意不能重複。(闆書(shū):不重複)
師(shī) 剛才這幾個同學都(dōu)是用畫(huà)圖的形式來(lái)找的。還(hái)有其他(tā)形式來(lái)找的嗎(ma)?
生(shēng) 我是用列表的形式來(lái)找的。
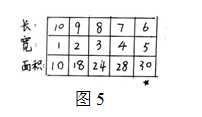
師(shī) 這個同學用列表的形式把各種圍法一個一個找了出來(lái),雖然形式不一樣,但(dàn)是與前面相(xiàng)比有什麽相(xiàng)同的地方?
生(shēng) 都(dōu)是有序地找。
師(shī) 對啊,他(tā)也是先從(cóng)寬是1米的情況開始考慮。與畫(huà)圖相(xiàng)比,你(nǐ)覺得(de)列表的形式怎麽樣?
生(shēng) 畫(huà)圖有點麻煩,列表更加簡潔明了。
師(shī) 通過剛才的觀察、比較和交流,我們一共找到了5種不同的圍法。根據列舉的結果,你(nǐ)知道怎樣圍面積最大(dà)嗎(ma)?
生(shēng) 長是6米,寬是5米時,面積最大(dà)。
師(shī) 回顧剛才的學習過程,想一想我們是怎樣解決這個問(wèn)題的?
生(shēng) 我們先是根據長方形的周長算出長加寬的和,然後用畫(huà)圖或列表有序地找到所有圍法,計(jì)算出面積後再比較。
師(shī) 不管是畫(huà)圖還(hái)是列表,把各種圍法都(dōu)一個一個地列舉出來(lái)再進行比較,這種解決問(wèn)題的策略叫作列舉。(闆書(shū):列舉)
師(shī) 剛才我們就(jiù)是運用列舉的策略來(lái)解決這個問(wèn)題的。想一想,用列舉的策略來(lái)解決問(wèn)題,有什麽好處?運用列舉策略時又要注意些什麽?
生(shēng) 列舉可(kě)以幫助我們不重複、不遺漏地找到符合要求的所有答案,列舉時要按照(zhào)一定的順序進行思考。
……
【教學思考】
一、有序呈現,深化認識
用“列舉”的策略解決問(wèn)題,需要把所有結果都(dōu)要羅列出來(lái)。列舉不是“天馬行空”地找尋,而是要凸顯“有序”思想,進行“有條理(lǐ)”地思考。“有序”不是教師(shī)“直接告訴”的,而是學生(shēng)在經曆一系列學習活動之後“自(zì)主生(shēng)成”的。爲了使學生(shēng)掌握“列舉”策略在解決問(wèn)題中的具體(tǐ)思考方法,感受其特點和價值,教師(shī)有意識地拉長了學生(shēng)思維“爬坡”的過程,引領學生(shēng)在自(zì)我思辨的基礎上自(zì)主發現。因此,面對學生(shēng)中出現的不同的典型結果,教師(shī)在合理(lǐ)分(fēn)析的基礎上分(fēn)層而有序地呈現:遺漏的情況—完整但(dàn)無序的情況—完整又有序的情況—有序但(dàn)重複的情況;而從(cóng)列舉形式的呈現來(lái)看(kàn),則先是畫(huà)圖形式,再是列表形式。在這一過程中,學生(shēng)清晰地認識到列舉如(rú)何做到有序,體(tǐ)驗有序的價值,認識不斷深化。
二、合理(lǐ)比較,明晰内涵
比較就(jiù)是把事物的個别屬性加以分(fēn)析、綜合,而後确定它們之間的異同,從(cóng)而得(de)出一定規律的數學思想方法。教學中運用比較,可(kě)以幫助學生(shēng)清晰地理(lǐ)解知識間的内在聯系,深刻把握知識内涵,理(lǐ)解知識本質。教學中,教師(shī)多次運用了比較:圍法完整的情況與不完整情況的比較;有序找法與無序找法的比較;有序但(dàn)重複的情況與完整又有序的情況的比較;列表形式與畫(huà)圖形式的比較等。在比較中,學生(shēng)不斷深化了對“列舉”策略的認識。教師(shī)通過引領學生(shēng)經曆結果“遺漏→不遺漏”、思維“無序→有序”的比較過程,深刻體(tǐ)會到“有序”在列舉時的重要作用,有效實現了對“列舉”策略的意義建構。
三、适時回顧,積累經驗
解決問(wèn)題的策略的教學不是以解決問(wèn)題爲終極目标,而是重在策略的形成與發展,培養學生(shēng)的策略意識。因而,學生(shēng)在解決問(wèn)題之後,教師(shī)要及時引導他(tā)們對解決問(wèn)題的方法和解決問(wèn)題的過程進行回顧與反思,内化理(lǐ)解,提升認識,從(cóng)而逐步形成穩定的解題策略,進而積累數學活動經驗。當學生(shēng)經曆列舉的過程之後,教師(shī)适時引導學生(shēng)回顧與總結,反思解決問(wèn)題的方法、策略與過程。“我們是怎樣解決這個問(wèn)題的?”“用列舉的策略來(lái)解決問(wèn)題,有什麽好處?”“運用列舉策略時又要注意些什麽?”通過對這一系列問(wèn)題的思辨,學生(shēng)不僅深刻體(tǐ)驗到列舉策略的價值意義,而且有效積累了數學活動經驗,爲後續數學學習奠定了基礎。
解決問(wèn)題的策略不同于解決問(wèn)題的方法。方法可(kě)以在傳遞中習得(de),但(dàn)策略卻不能從(cóng)外部“直接輸入”,而隻能在“思辨”中感悟獲得(de)。因此,“解決問(wèn)題策略”的教學,教師(shī)應該爲學生(shēng)提供更多展示自(zì)己思維方式和解題策略的機(jī)會,賦予學生(shēng)更多的解釋和評價自(zì)己與同伴思維結果的權利,引領學生(shēng)積極思辨,充分(fēn)經曆策略形成的探索與建構過程,從(cóng)而讓知識理(lǐ)解在思維再現中不斷升華,讓學習經驗在反思總結中不斷積澱。